RL Algorithm: RLHF & DPO

Reinforcement Learning (RL) algorithms for LLM alignment with human preferences: RL from Human Feedback (RLHF) and Directed Preference Optimization (DPO).

DPO arXiv Link👈

RLHF

LLM training typically consists of three phases:

1. Pre-train: train the model with large scale internet raw data through self-supervised learning methods (e.g. next word prediction etc.), providing the model with vast foundational and general knowledge, and the ability to complete the given content.
2. SFT: more strict and oriented supervised training with labelled output given input data, usually used to provide the model with text generation abilities in specific context format, e.g. chat.
3. RLHF: align the model's output with human preferences and intentions through reinforcement learning, mitigating the generation of biased, harmful or other types of sub-optimal content.

The problem of RLHF is how to incorporate human preferences in LLM training.

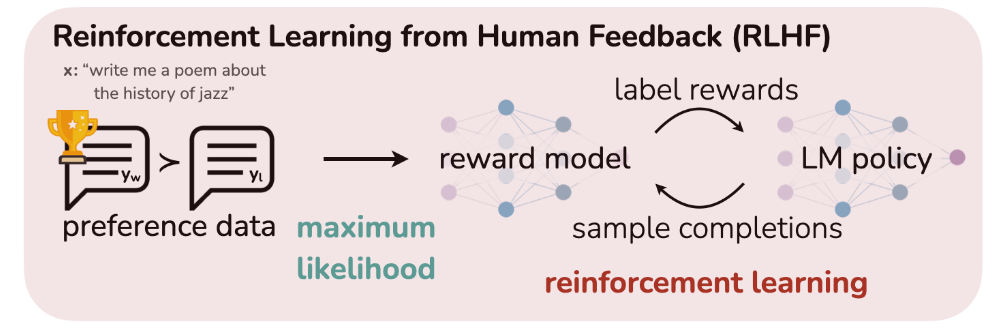
Preference Reward Model (RM)

The reward model typically plays a crucial role in RL, which provides the reward signal and decides the direction of the model optimization. Here, we can incorporate the human preference information into the reward model, thus providing the guidance for LLM alignment.

Here we talk about one types of applicable model that can model the human preference as a probability problem, Bradley-Terry model:

\[ p^*(y_1 \succ y_2 | x) = \frac{\exp(r^*(x,y_1))}{\exp(r^*(x,y_1))+\exp(r^*(x,y_2))} \]

This can be expressed as a sigmoid function:

\[ \frac{1}{1+\exp(-(r^*(x,y_1)-r^*(x,y_2)))} = \sigma (r^*(x, y_1) - r^*(x, y_2)) \]

where the \(r^*\) is the target reward function that can provide a score for each output \(y\) given \(x\).

Note: Plackett-Luce ranking model can be used if we have access to several ranked answers.

Then, we can make the loss function for the reward model:

\[ \mathcal{L}_R(r_{\phi}, \mathcal{D}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} [ \log \sigma ( r_{\phi}(x, y_w) - r_{\phi}(x, y_l) ) ] \]

where the \(r_{\phi}\) is the reward model being trained, \(\mathcal{D}\) is the dataset, while \(y_w\) and \(y_l\) are the preferred response and dispreferred one, respectively.

Explanation: the objective of the loss function is to maximize the difference between the rewards of the preferred response and the dispreferred one.

RL with Preference RM

After training the RM, it can be used directly in the RL training of the LLM, with the objective:

\[ \max_{\pi_{\theta}} \mathbb{E}_{x \sim \mathcal{D}, y \sim \pi_{\theta}(y \mid x)} [r_{\phi}(x, y)] - \beta D_{\text{KL}} [\pi_{\theta}(y \mid x) \,\|\, \pi_{\text{ref}}(y \mid x)] \]

where the KL constraint is introduced to prevent the model from deviating too far from the distribution on which the reward model is accurate, and maintaining the generation diversity and preventing mode-collapse to single high-reward answers.

In other words, it is for preventing the reward hacking.

Note: The policy and reference models are typically initialized to the SFT model.

In practice, the final reward function, integrated with the KL constraint, can be modelled as:

\[ r(x,y) = r_{\phi}(x,y) - \beta ( \log \pi_{\theta}(y \mid x) - \log \pi_{\text{ref}}(y \mid x)) \]

Then, we can use RL algorithms like PPO to train the policy model.

DPO

The Direct Preference Optimization (DPO) trains the LLM by utilizing the preference information directly, without the need of a reward model and RL loop, by mapping from reward functions to corresponding optimal policies.

It replaces the 2-step procedure: 1. training a reward model, and 2. using it to train a policy, with just one step: fine-tuning the policy directly with the guidance of preferences.

Objective Derivation

Under a reward function \(r\), the optimal solution to the KL-constrained reward maximization objective takes the form:

\[ \pi_r(y \mid x) = \frac{1}{Z(x)} \pi_{\text{ref}}(y \mid x) \exp ( \frac{1}{\beta} r(x,y)) \]

where \(Z(x) = \sum_y \pi_{\text{ref}}(y\mid x) \exp (\frac{1}{\beta}r(x,y))\) is the partition function.

However, we can represent the reward function \(r\) in terms of its corresponding optimal policy \(\pi_r\), the reference policy \(\pi_{\text{ref}}\), and \(Z(x)\):

\[ r(x,y) = \beta \log \frac{\pi_r(y \mid x)}{\pi_{\text{ref}}(y \mid x)} + \beta \log Z(x) \]

Then, we can apply this reparameterization to the ground-truth reward \(r^*\) and its corresponding optimal policy \(\pi^*\) in the Bradley-Terry model, and the partition function cancels with the subtraction:

\[ p^*(y_1 \succ y_2 \mid x) = \frac{1}{1 + \exp \left( \beta \log \frac{\pi^*(y_2 \mid x)}{\pi_{\text{ref}}(y_2 \mid x)} - \beta \log \frac{\pi^*(y_1 \mid x)}{\pi_{\text{ref}}(y_1 \mid x)} \right)} \]

Now that we have the probability of human preference data in terms of the optimal policy rather than the reward model, we can formulate a maximum likelihood objective for a parametrized policy \(\pi_\theta\):

\[ \mathcal{L}_{\text{DPO}}(\pi_{\theta}; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \frac{\pi_{\theta}(y_w \mid x)}{\pi_{\text{ref}}(y_w \mid x)} - \beta \log \frac{\pi_{\theta}(y_l \mid x)}{\pi_{\text{ref}}(y_l \mid x)} \right)\right] \]

This way we are fitting a reparametrized Bradley-Terry model which can optimize directly the policy.

Update Analysis

We can look into the update of DPO by checking its gradient:

\[ \begin{aligned} & \nabla_{\theta} \mathcal{L}_{\text{DPO}}(\pi_{\theta}; \pi_{\text{ref}}) = \\\\ & - \beta \mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \underbrace {\sigma \left( \hat{r}_{\theta}(x, y_l) - \hat{r}_{\theta}(x, y_w) \right) }_{\substack{\text{higher weight when}\ \text{reward estimation is wrong}}} \left[ \underbrace {\nabla_{\theta} \log \pi_{\theta}(y_w \mid x)}_{\substack{\text{increase likelihood of } y_w}} - \underbrace {\nabla_{\theta} \log \pi_{\theta}(y_l \mid x)}_{\substack{\text{decrease likelihood of } y_l}} \right] \right] \end{aligned} \]

where \(\hat{r}_{\theta}(x, y) = \beta \log (\frac{\pi_\theta (y \mid x)}{\pi_{\text{ref}}(y \mid x)})\).

The update increases the likelihood of the preferred completions \(y_w\) and decreases the likelihood of dispreferred completions \(y_l\).

More importantly, the examples are weighed by how much higher the implicit reward model \(\hat{r}_\theta\) rates the dispreferred completions, scaled by \(\beta\), i.e., how incorrectly the implicit reward model orders the completions, accounting for the strength of the KL constraint.