Linear Algebra Note#1：Row, Column & Matrix

Posted on In

This note is based on MIT 18.06📒

Content

Row & Column picture

Given two linear equations with two unknowns \(x\) and \(y\):

\[ \begin{aligned} 2x-y&=0\\\\ -x+2y&=3 \end{aligned} \]

The geometric view of the rows (i.e. the equations themselves) looks like:

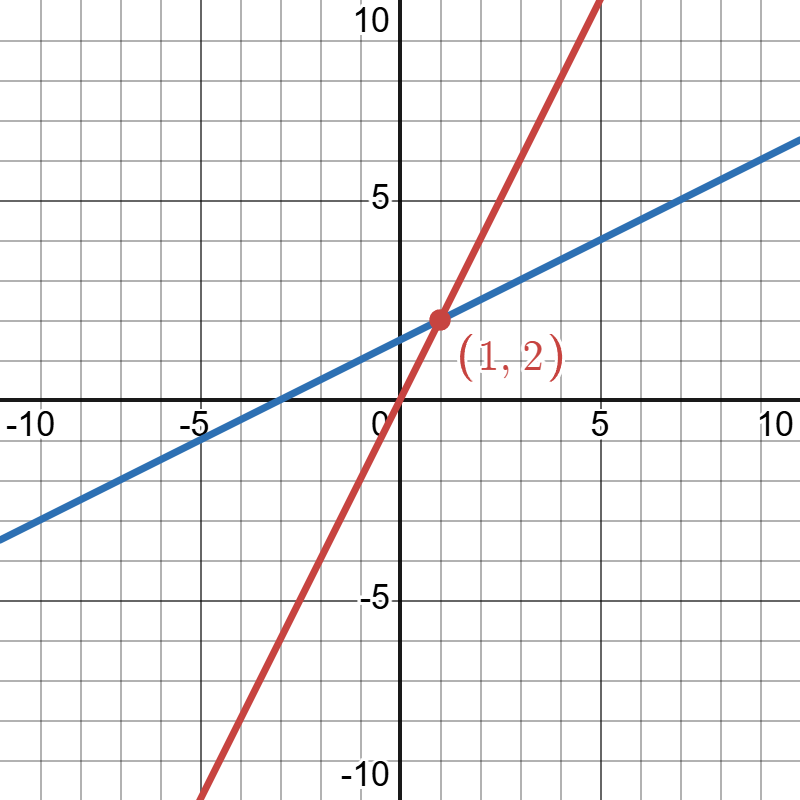
  • each equation is expressed as a straight line
  • the solution of the equations is the intersection of the lines

While the column picture can be expressed as:

\[ \begin{gathered} x \begin{bmatrix} 2 \\\\ -1 \end{bmatrix} +y \begin{bmatrix} -1 \\\\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\\\ 3 \end{bmatrix} \end{gathered} \]

  • the coefficients in the equations are viewed as column vectors
  • the combination of the equations becomes the linear combination of these column vectors
  • the solution is the coefficients (\(x\), \(y\)) of the right combination

What are all the linear combinations of the column vectors? The results of all the combinations mean all possible right hand side vector, which usually make up a space of the same dimension as the number of equations/unkowns (a 2-d plane in this case).

How about a 3x3 comb of linear equations?

\[ \begin{aligned} 2x-y&=0\\\\ -x+2y-z&=-1\\\\ -3y+4z&=4 \end{aligned} \]

The row picture becomes 3-d, with each equation a 2-d plane, and the intersection is a point (means there's only one single solution in this case):

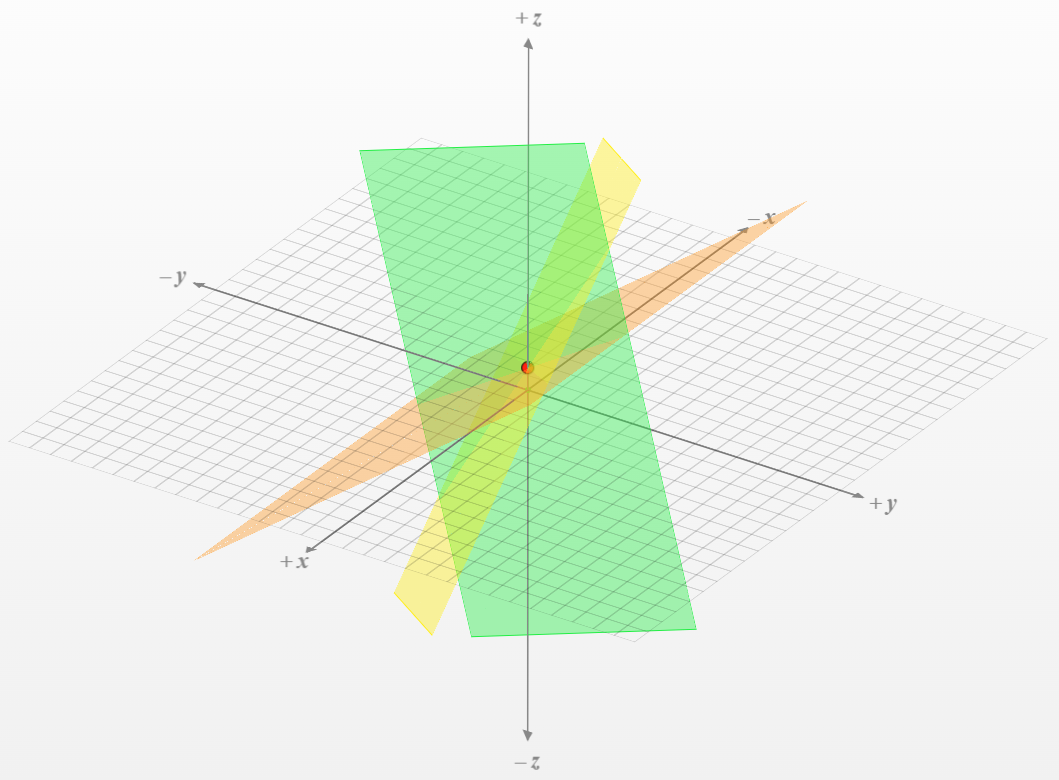
The column picture is still a linear combination question:

\[ \begin{gathered} x \begin{bmatrix} 2 \\\\ -1 \\\\ 0 \end{bmatrix} +y \begin{bmatrix} -1 \\\\ 2 \\\\ -3 \end{bmatrix} +z \begin{bmatrix} 0 \\\\ -1 \\\\ 4 \end{bmatrix} = \begin{bmatrix} 0 \\\\ -1 \\\\ 4 \end{bmatrix} \end{gathered} \]

Solution space

Can I solve the equations for every right-hand side?

  • i.e. can I solve \(Ax=b\) for every \(b\) ?
  • *Column perspective: For a \(n\times n\) combination of equations (\(n\) unknowns and \(n\) equations), do the linear combinations of the column vectors fill the whole \(n\)-d space?

Singular case: in \(3\times 3\) case, if all three column vectors lie in the same plane, the \(b\) vector lies outside the plane isn't accessible.

Formal explanation: not all \(b\) are accessible when some columns are not independent, i.e. \(n\) columns but are expressive same as \(n-1\) or even less columns, which means at least one of them gives nothing new about the dimensions.

  • In \(9\times 9\) case, if columns express like 8 columns, then only the 8-d plane inside the 9-d space is accessible.

Matrix * vector

\[ Ax=b \]

Column view:

\[ \begin{gathered} \begin{bmatrix} 2 & 5 \\\\ 1 & 3 \end{bmatrix} \begin{bmatrix} 1 \\\\ 2 \end{bmatrix} = 1 \begin{bmatrix} 2 \\\\ 1 \end{bmatrix} + 2 \begin{bmatrix} 5 \\\\ 3 \end{bmatrix} = \begin{bmatrix} 12 \\\\ 7 \end{bmatrix} \end{gathered} \]

  • \(Ax\) is a linear combination of the columns of \(A\)

Row view:

\[ \begin{aligned} 2\times 1 + 5\times 2 & = 12 \\\\ 1\times 1 + 3\times 2 & = 7 \end{aligned} \]

  • each row of \(A\) does a dot product with the vector \(x\)